Методика биометрической обработки

Промеры и взвешивания позволяют нам определить индивидуальные особенности экстерьера лошади. Однако иногда требуются обобщенные данные о промерах группы лошадей, например, необходимо сравнить кобыл разных конных заводов или колхозных ферм, сравнить промеры молодняка, выращенного в одном хозяйстве, с промерами молодняка другого хозяйства или развитие приплода данного года с развитием приплода предыдущего года, произвести зоотехническое описание отдельных групп конского поголовья.

Для такого сравнения вычисляют среднюю обобщенную величину какого-либо показателя (среднюю арифметическую из ряда цифр) по формуле:

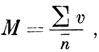
где М - средняя арифметическая;

Σ - знак суммирования;

υ - варианты;

n - число особей в обработке.

Для определения средней арифметической - М, таким образом, необходимо сложить все варианты и разделить их на число особей.

Например, высота в холке 15 кобыл на племенной ферме рысистых лошадей равна: 156, 160, 154, 169, 148, 150, 159, 157, 153, 158, 152, 159, 154, 160, 155 см. Индивидуальные показатели высоты в холке в данном случае будут вариантами (υ).

Сложив эти варианты и разделив их на число особей (n = 15), мы получим величину средней арифметической М = 156,3 см.

Помимо средней арифметической М, для характеристики кобыл данного хозяйства по росту в холке необходимо знать размах колебаний (L-L), т. е. наибольший и наименьший промер, который в данному случае будет равен 148-169 см. Такой способ вычисления средней применяется в том случае, когда количество вариантов невелико - в пределах 10-15 голов.

Когда же в группе десятки и сотни голов животных, вычисление средней связано со сложением большого количества двузначных и трехзначных цифр. В таких случаях М вычисляют особым способом моментов, позволяющим избежать скучных и утомительных подсчетов. Способ моментов (помимо средней арифметической М) позволяет вычислить без особого труда еще ряд необходимых показателей, характеризующих вариационный ряд:

1) m - вероятную ошибку среднего арифметического М;

2) σ (сигму) - среднее квадратическое отклонение;

3) c - коэффициент вариации.

Вычисление по способу моментов М и других констант мы покажем на примере обработки вариационного ряда веса при рождении орловских рысистых жеребят.

Предположим, живой вес жеребят следующий (в кг): 51, 48, 58, 42, 55, 48, 48, 54, 44, 52, 54, 50, 54, 53, 45, 50, 51, 57, 48, 43, 56, 57, 46, 57, 50, 48, 51, 58, 48, 53, 57, 51, 53, 52, 59, 47, 55, 57, 48, 59.

Первое, что нужно сделать при обработке вариационного ряда, - это определить число животных (n) и размах колебаний (L-L), которые в данном случае будут:

Затем, руководствуясь показанием L-L, все цифры вариационного ряда надо разбить на классы с таким расчетом, чтобы весь вариационный ряд разбился на 8-12 классов.

Разность между наибольшей и наименьшей величиной варианта будет 17(59-42 = 17), поэтому в данном случае за величину классового промежутка целесообразно взять 2 кг, в связи с чем наш вариационный ряд разобьется на 9 классов: 42-43, 44-45, 46-47, 48-49, 50-51, 52-53, 54-55, 56-57, 58-59.

Далее, вычерчивают следующую вспомогательную таблицу (табл. 7).

Таблица 7. Вспомогательная таблица для вычисления по способу моментов

В первую графу вписывают установленные классы. Во второй графе проставляют количество животных в каждом классе - частоты (p). Так, в классе 42-43 кг у нас было 2 животных, в классе 44-45 кг - 2 животных и т. д.

После этого произвольно выбирают условный средний класс (А), от которого ведется последующий подсчет. Выбор условного среднего не отражается на точности вычисления, но чем ближе выбранный класс будет к действительной средней, тем проще последующие подсчеты, px. В данном случае берут за условный средний класс 50-51. Этот класс в первой графе обводят круговой чертой или отличают каким-либо другим способом.

Затем в третью графу (x) вписывают положительные и отрицательные уклонения от избранной условной средней. Вне зависимости от величины классового промежутка уклонения от класса к классу выписывают равными единице.

Далее, заполняют четвертую графу - произведение частоты на уклонение (px). После этого складывают сначала все отрицательные, затем

положительные цифры четвертой графы (px) и вычисляют общую сумму px. В данном случае

В результате деления Σpx на число животных n получают вспомогательную величину-момент первой степени V₁:

Вычисление средней арифметической М производят по формуле:

где А - произвольно выбранная условная средняя, V₁ - момент первой степени и К - величина классового промежутка.

Если величина классового промежутка больше или меньше единицы, за условную среднюю надо брать среднее арифметическое между крайними цифрами классов. В нашем примере условный средний класс 50-51 следовательно, А будет равно 50,5 кг.

Таким образом,

На первый взгляд этот способ вычисления может показаться сложным. Однако после 2-3 упражнений сразу приобретается некоторый навык, и вычисление средней по этому способу занимает буквально несколько минут.

Чтобы определить последующие показатели вариационного ряда (m, σ, с), необходимо вычислить момент второй степени V₂. Для этого вспомогательную таблицу дополняют еще одной графой, в которой производят вычисление произведения частот на квадраты уклонений - px².

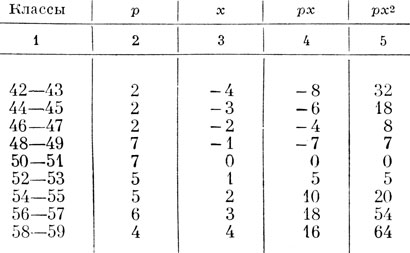
Таблица 8. Вспомогательная таблица вычисления показателей вариационного ряда

px² вычисляют путем умножения цифр третьей графы (x) на цифры четвертой графы (px) и, таким образом, заполняют пятую графу. Цифры пятой графы всегда будут положительными. Далее берется сумма px². В данном случае

Для определения момента второй степени (V₂) Σpx² делится на число животных n:

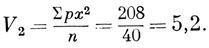
Среднее квадратическое отклонение - σ (сигма) - вычисляется по формуле:

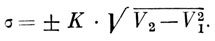
В нашем примере:

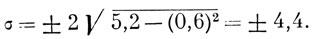
Итак, среднее квадратическое отклонение данного вариационного ряда σ = ±4,4.

Среднее квадратическое отклонение даст нам представление об относительной изменчивости того или иного изучаемого показателя. При этом надо учитывать, что о является именованным числом и величина σ в значительной мере зависит и от самой величины этого числа. Поэтому σ для вариационного ряда, например живого веса, будет всегда больше, чем σ обхвата пясти. Пользуясь σ, мы можем сравнивать изменчивость только какого-либо одного показателя у лошадей двух заводов, колхозов, двух пород и т. п.

Иногда необходимо получить представление об относительной изменчивости двух показателей, например живого веса и обхвата пясти, у одной и той же группы лошадей.

Тогда вычисляют коэффициент вариации С по формуле:

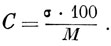
Таким образом, коэффициент вариации показывает величину среднего квадратического отклонения (σ) в процентах к средней арифметической для данного ряда (М).

При изучении пород лошадей обычно никогда не обследуют все поголовье, а для характеристики породы измеряют лишь какую-то группу животных этой породы. Чем большее количество животных изучается, тем точнее показания М - средней арифметической по данному признаку.

Однако точность показаний М зависит не только от количества животных, но и от изменчивости изучаемого признака. Признаки менее изменчивые дают большую точность показаний М при меньшем количестве животных.

Для определения степени точности М вычисляют условный показатель точности m, называемый вероятной ошибкой средней арифметической (М), по формуле:

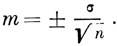
Таким образом, вероятная ошибка m прямо пропорциональна а и обратно пропорциональна n.

Нередко требуется знать степень достоверности различий средних арифметических по двум вариационным рядам. Например, сравнивается средняя высота в холке жеребят в годовалом возрасте в текущем году с высотой в холке годовалых жеребят в предыдущем году. Достоверность разницы при этом вычисляется по формуле:

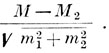
Если отношение разности средних арифметических к корню квадратному из суммы квадратов ошибок будут больше 3, разница считается статистически достоверной. Однако все это имеет лишь условное значение. Очень часто в зоотехнических опытах или при обработке производственных материалов разница оказывается недостоверной лишь из-за малого количества животных в сравниваемых группах. То же явление, изученное на большем количестве объектов, может показать статистическую достоверность различия.

Для определения взаимной зависимости двух признаков при биометрической обработке материалов пользуются вычислением коэффициента корреляции. При изучении экстерьера пород коэффициент корреляции вычисляется в том случае, когда требуется выявить взаимосвязь между двумя признаками, например между длиной шеи и длиной ног, длиной головы и обхватом пясти и т. д. Коэффициент корреляции вычисляют тогда, когда нужно установить взаимную связь различных явлений, например живого веса жеребят при рождении с весом этих жеребят в зрелом возрасте или веса новорожденных с весом матерей и т. п.

Покажем способ вычисления коэффициента корреляции (r) на примере вычисления корреляции между весом жеребят при рождении и весом их материй. Для этого воспользуемся следующим рядом пар цифр, из которых первая цифра в паре - живой вес жеребенка, а вторая-вес матери (в кг): 51-483, 48-487, 58-481, 42-462, 55-538, 48-480, 48-478, 54-509, 52-533, 54-577, 50-510, 54-486, 53-526, 44-450, 45-470, 50-460, 51-468, 57-598, 48-469, 43-420, 56-534, 57-550, 46-500, 57-545, 50-491, 48-444, 51-532, 58-520, 48-496, 53-552, 47-450, 57-544, 51-520, 53-597, 52-527, 59-555, 55-547 57-529, 48-524, 59-585.

При вычислении r приходится иметь дело с двумя свойствами, из которых одно (в данном случае вес матери), основное свойство - a и другое, зависимое - b (определение основного и зависимого свойства является произвольным).

Сначала определяем L-L по рядам a и b. В данном примере:

В обоих случаях n = 40.

Далее определяем величины классовых промежутков для рядов a и b. Для удобства вычисления желательно иметь одинаковое количество классов в обоих рядах (желательно 8-12 классов).

По ряду а установим классовый промежуток в 20 кг, по ряду b, как и в предыдущем случае, - 2 кг.

Затем вычерчивается корреляционная решетка, сверху и слева которой выписываются значения классов ряда a и b в возрастающей последовательности, а справа и снизу оставляются свободные графы для записи уклонений (x).

В месте пересечения граф рядов a и b решетки заполняем цифрами (частотами p). Например, жеребенок имеет вес 51 кг, его мать - 483 кг; частота (p) проставляется на пересечении граф 50-51 и 480-499 и т. д.

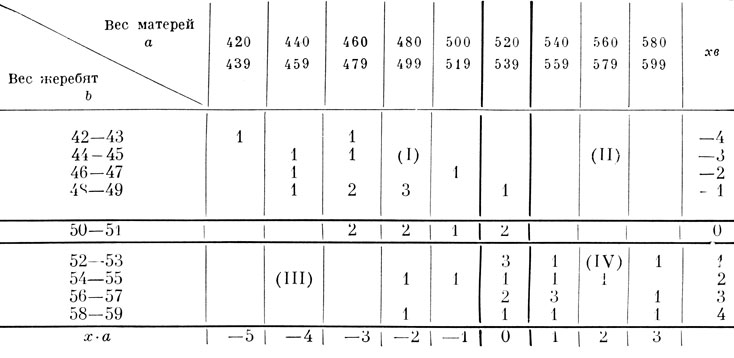
Таблица 9. Корреляционная решетка

Уже расположение цифр в решетке дает первое представление о корреляции. Если корреляции не имеется, цифры окажутся рассеянными по всей решетке. Если корреляция положительная, как в нашем примере, цифры расположатся преимущественно по диагонали слева вниз направо. При отрицательной корреляции (обратной зависимости) цифры расположатся по диагонали справа вниз налево.

Далее, для ряда а и b произвольно, но по возможности наиболее близко к истинной средней, выбираем приближенные средние и от них как и в предыдущем случае, выписываем уклонения (х) без учета величины классового промежутка. Нолевые классы разбивают решетку на четыре квадранта: I, II, III, IV. Частоты каждого квадранта умножаем на два уклонения. Цифры, попадающие в нолевые классы, не учитываются. Результаты вычисления вписываем во вспомогательную таблицу.

Вспомогательная таблица

Затем берем общую сумму произведений частот па уклонения рядов a и b, которую получаем путем сложения цифр всех четырех квадрантов.

В данном примере

После этого приступаем к вычислению для каждого ряда в отдельности моментов первой (V₁) и второй (V₂) степени и σ. Эти вычисления производим по методу, изложенному выше, с той лишь разницей, что при вычислении σ не производим умножения на величину классового промежутка.

По ряду b воспользуемся готовыми вычислениями, сделанными выше (при определении показателей вариационного ряда живого веса жеребят). По вариационному ряду b V₁=0,6, V₂ = 5,2.

Пользуясь этими константами, вычисляем σ по несколько отличной от предыдущей формуле:

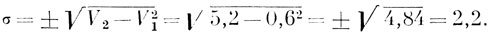
Пользуясь изложенным выше методом, определяем V₁, V₂ и σ для ряда а (живой вес матерей).

В данном случае для ряда а:

После этого производим вычисление коэффициента корреляции по формуле:

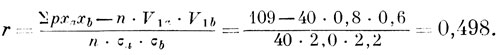
Если между признаками имеется прямая взаимосвязь, коэффициент корреляции будет положительной величиной, при обратной зависимости - отрицательной.

Во всех случаях коэффициент корреляции будет в пределах единицы (от 0 до ±1,00). В нашем примере установлена прямая взаимосвязь - положительная корреляция живого веса новорожденных жеребят с весом их матерей.